マニピュレータ制御①~順運動学、逆運動学~
制作過程(ロボットアーム)
5自由度のマニピュレータを制作、制御します。マニピュレータで物を掴んだり、手書き文字を書いたり、イラストを描いたりすることが最終的な目標です。
あくまで趣味の延長として取り組んでいますが、将来的に私の研究の実証実験などで利用できれば一石二鳥と考えています。
また、サーボを手に入れるのに時間がかかりそうなので、まずは制御から取り掛かります。
この記事では、一度にマニピュレータの制御についてまとめると文章量が膨大になるため複数回に分けて記述します。
今回は、マニピュレータの先端速度を制御する術について書いていきます。
一般に順運動学とは、関節の角速度から先端速度や先端姿勢を求めることであり、逆運動学とは、先端速度や先端姿勢から関節の角速度を求めることをいいます。
今回作成するマニピュレータでは、直接的に操作できるパラメータは各関節のサーボの角速度であるため、マニピュレータの先端速度、姿勢を実現するために必要な関節角速度を求めることができる逆運動学を解くことが目標です。
そのためにまずは順運動学から計算して、関節角速度から先端速度、姿勢に変換する変換行列である「ヤコビアン」を計算します。
マニピュレータの定義
今回想定しているロボットアームはこのような5自由度の関節をもつマニピュレータです。
手先については、タスクに応じて手先にグリッパなどを取り付けたいと考えています。
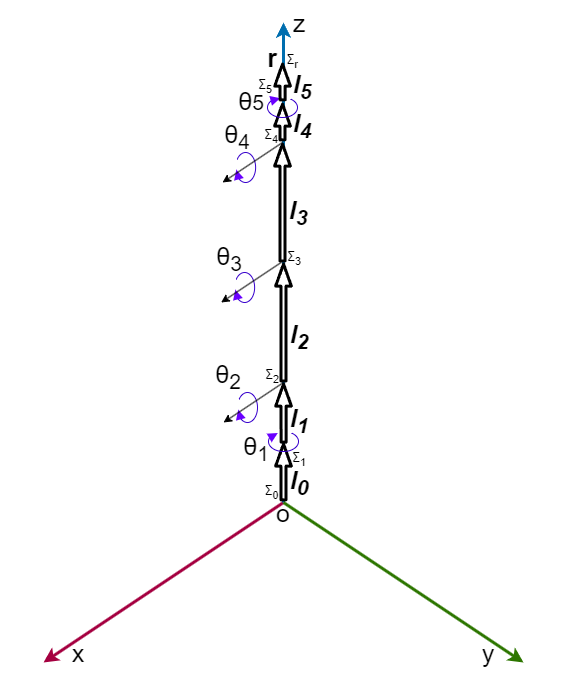
5自由度マニピュレータのモデル
| 文字 | 定義 |
|---|---|
| $\bm{r}$ | 先端の座標ベクトル [cm] |
| $θ_i$ | 関節$i$の角度 [rad] |
| $\bm{l_i}$ | リンク$i$の長さのベクトル [cm] |
| $\Sigma_i$ | 座標系$i$ |
太い矢印部分がマニピュレータの本体になり、回転軸が設定されている箇所に関節が存在します。
また、$\Sigma_i$の原点から$\Sigma_g$の原点までのベクトルを$\bm{P_i^g}$と定義します。
続いて、3次元(SE(3))空間での回転行列、手先姿勢は以下のように定義します。
| 文字 | 定義 |
|---|---|
| $\bm{R_i^g}$ | $\Sigma_i$から見た$\Sigma_g$の姿勢を表す回転行列 |
| $\alpha$ | 手先の姿勢 Roll [rad] |
| $\beta$ | 手先の姿勢 Yaw [rad] |
このとき、$\bm{R_0^1}$、$\bm{R_4^5}$はz軸周りの回転であり、$\bm{R_1^2}$、$\bm{R_2^3}$、$\bm{R_3^4}$はx軸周りの回転であることから、回転行列は以下の通りです。
※視認性を良くするため、cos($θ_i$)は$c_i$、cos($θ_i$)*cos($θ_g$)は$c_{ig}$と記述します(sinも同様)
$$ \bm{R_0^1} = \bm{R_4^5} = \begin{pmatrix} c_i & -s_i & 0 \\ s_i & c_i & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} $$ $$ \bm{R_1^2} = \bm{R_2^3} = \bm{R_3^4} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & c_i & -s_i\\ 0 & s_i & c_i \\ \end{pmatrix} $$
順運動学解の導出
$\Sigma_4$から$\Sigma_r$までは、以下のように表すことができます。 $$ \bm{P_4^r} = \bm{R_4^5} \cdot \bm{l_5} + \bm{l_4} $$ 次に$\bm{P_3^r}$は、先ほど求めた$\bm{P_4^r}$を使用して以下のように表すことができます。 $$ \bm{P_3^r} = \bm{R_3^4} \cdot \bm{P_4^r} + \bm{l_3} $$ $$ = \bm{R_3^4} \cdot \bm{R_4^5} \cdot \bm{l_5} + \bm{R_3^4} \cdot \bm{l_4} + \bm{l_3} $$ 同様に繰り返していくことで、$\bm{P_0^r}$は以下のように表すことができます。 $$ \bm{P_0^r} = \bm{R_0^1} \cdot \bm{R_1^2} \cdot \bm{R_2^3} \cdot \bm{R_3^4} \cdot \bm{R_4^5} \cdot \bm{l_5} $$ $$ +\bm{R_0^1} \cdot \bm{R_1^2} \cdot \bm{R_2^3} \cdot \bm{R_3^4} \cdot \bm{l_4} $$ $$ +\bm{R_0^1} \cdot \bm{R_1^2} \cdot \bm{R_2^3} \cdot \bm{l_3} $$ $$ +\bm{R_0^1} \cdot \bm{R_1^2} \cdot \bm{l_2} $$ $$ +\bm{R_0^1} \cdot \bm{l_1} $$ $$ +\bm{l_0} $$
以上により、$\bm{P_0^r}$が求まりました。
実際に計算した値がこちらです。(変数th$i$は、$θ_i$)
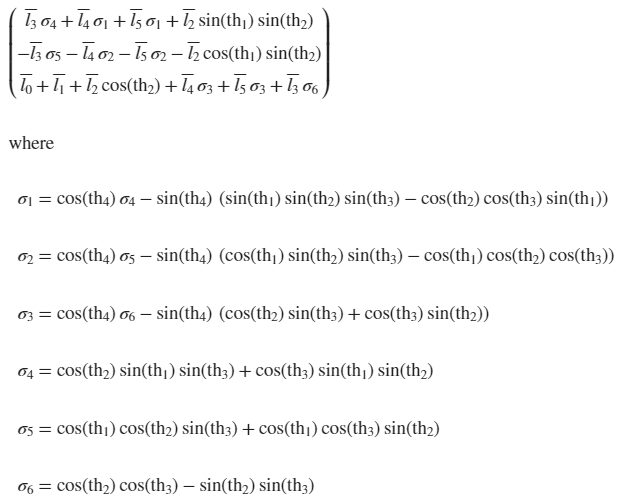
MATLABで計算した$\bm{P_0^r}$
続いては、$\bm{P_0^r}$の式から実際にヤコビアンを計算していきます。
そのためにまずは、以下の$\bm{A}$、$\bm{G}$を定義します。
$$ \bm{A} = \frac{d}{dt} \begin{pmatrix} \bm{P_0^r} \\ \alpha \\ \beta \\ \end{pmatrix} $$ $$ \bm{G} = \frac{d}{dt} \begin{pmatrix} θ_1 \\ θ_2 \\ θ_3 \\ θ_4 \\ θ_5 \\ \end{pmatrix} $$
そして、$\bm{P_0^r}$の時間微分を利用することで、以下の式が成り立つようなヤコビアン$\bm{J}$を求めます。
$$ \bm{A} = \bm{J} \cdot \bm{G} $$ $$ \bm{J} = \begin{pmatrix} \frac{d}{dθ_1}\bm{P_0^r} & \frac{d}{dθ_2}\bm{P_0^r} & \frac{d}{dθ_3}\bm{P_0^r} & \frac{d}{dθ_4}\bm{P_0^r} & \frac{d}{dθ_5}\bm{P_0^r} \\ 0 & 1 & 1 & 1 & 0 \\ 1 & 0 & 0 & 0 & 1 \\ \end{pmatrix} $$
実際に計算されたヤコビアンは式が長すぎるので、ここでは省略します。
逆運動学解の導出
最後にやっと逆運動学解が求められます。
逆運動学は、先端速度、先端姿勢から関節角速度を求められればよいので、以下のような式が成り立つ$\bm{J}^{-1}$を求めます。
$$
\bm{G} = \bm{J}^{-1} \cdot \bm{A}
$$
今回のマニピュレータは5自由度で手先
$
\bm{G}
$
を制御しようとしているため、求めたヤコビアン$\bm{J}$は特異姿勢以外では、正則な行列となるため逆行列が存在します。
逆行列が存在しているため、そのまま$\bm{J}$の逆行列を求めることができれば、$\bm{J}^{-1}$が逆運動学解になります。
(関節の数が多いマニピュレータなど、冗長性がある場合は、別の手段をとる必要がある)
実際に計算された逆ヤコビアンは式が長すぎるので、ここでは省略します。
まとめ
はじめに順運動学から計算していくことで、ヤコビアンを求め、その逆行列を計算して逆運動学解を求めました。
次回は、トルクの計算か制御システムを実装してリモコンで手先制御などを行う予定です。